Tracking movement path with magnetometer in Android

This time I wanted to learn Android development. I've tried to choose some interesting idea for test Android project. So i came to final project mission - drawing user movement path using magnetometer as a compass. You can use this app as a helper to orientation in unknown place or for example it can be used to chart scheme of apartments in some building. I've used this app to draw my flat scheme :-) You can download sources of this application from Google project hosting of my project. I've called this app PathRecorder :-) Structure of code:

FullscreenActivity.java

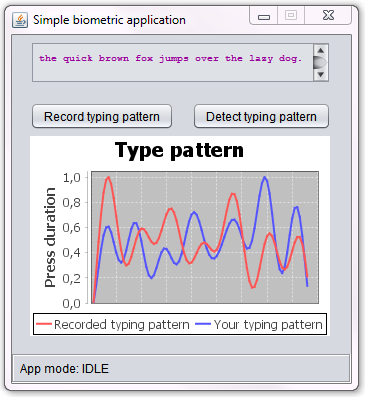
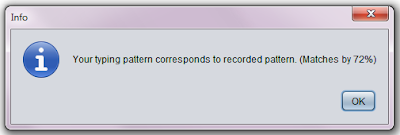
Basic usage of activity is: Creation/setup of view which will used for drawing; setup of UI interaction (On Touch listener,etc.); magnetometer sensor setup; initialization of various classes used for project (such as Storage of app data, MenuManager for showing user menu, etc.); starting some threads for program state monitoring.

MenuItem.java

Used for saving information about current active menu item in UI, such as - menu text and program state which will be fired when user will switch to this menu item. (All communication between application components goes through ProgramState object, it's like a state machine :-) )

MenuManager.java

Container for MenuItem class instances. Also holds logic for controlling menu system such as - switching current active menu item, loading menu bitmap resources, checking mouse click event and performing menu actions (changing active menu item, executing current item, etc.).

Movement.java

Holds class MovementStatistics, which is used for computing some information about current movement path, such as - time traveled in some compass direction, times user rotated clockwise or counter-clockwise, etc. Movement class itself stores LinkedList of user moves, appends nodes to this list as user travels in some direction, communicates to magnetometer sensor fetching current user direction relative to North, converts movement data into representation suitable for drawing movement path in a view (returns Path draw object for canvas).

Orientation.java

Implements SensorEventListener interface for getting data from magnetometer sensor. Performs all interaction with magnetometer sensor, such as - performing magnetometer calibration (detects accuracy of magnetometer, min/max values of magnetic field, checks for errors in calibration, for example there should be zero or minimum device tilting when in calibration mode, because tilting changes magnetometer output rapidly), calculates degrees to North pole according magnetometer field strength data and passes this information for compass drawing to view.

ProgramState.java

State machine of application - integrates all application components, so that all components could interact between each other and user interface. Also some threads monitors program state and changes it by calling "check..." method in ProgramState class (for example,- calibration monitor thread informs ProgramState when calibration is finished and UI can show menu for a user...).

SketchView.java

Exports drawing to bitmap. Performs drawing of visual elements in view such as,- compass, status bar, menu, user movement statistics, user movement path.

Storage.java

Exports user path drawing to JPG file. Loads/Saves magnetometer calibration data.

Vector2D.java

Wrapper for vector algebra (for example,- calculation of dot product of vectors, angle between vectors, vector normalization, vector addition, vector rotation, etc...).
Most important classes are Orientation.java and Movement.java.
--------------------------------------------
Orientation.java
--------------------------------------------
Encapsulates control of magnetometer sensor. Now I would like to talk a bit about how direction to North is calculated. Most important fact is that absolute maximum value of magnetic field strength along X axis points to west, and absolute maximum value of magnetic field strength along Y axis points to north. I.e. X axis in magnetometer measures magnetic field strength along west-east axis and Y magnetometer axis measures magnetic field strength along north-south axis. So by having these facts we can calculate direction to North. Consider this picture:

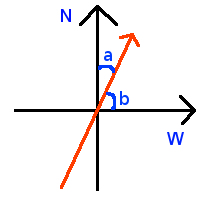
So by having magnetometer data we can calculate (a,b) angles in a following way:


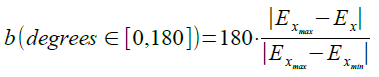
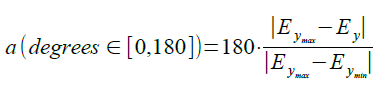
The only problem is that calculated angle a is in range 0,180 degrees, and we need full range of -180,+180 degrees. So we need to decide sign of a angle, which can be determined from angle b. By doing that we get full direction to North angle formula:

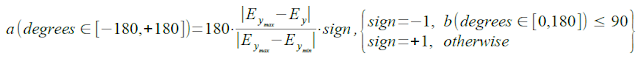
So we just need to find min,max values of magnetic field. This is achieved by magnetometer calibration in two phases. Phase 1 - simply measures fluctuation of magnetic field when device is stationary and extracts error of magnetic field magnitude. And second phase of calibration - collects magnetic field strength data when user is turning around itself (i.e. around Z axis). After 1 full rotation min,max values are extracted from this data.
-----------------------------------------
Movement.java
-----------------------------------------
This class collects user movement information in a form - How much time user traveled in some direction relative to North, by fetching magnetometer data using Orientation.java class. Later view which draws user movement path queries draw data from Movement.java class by calling method "getMovementDataForDraw()", which looks like this:

 public Object[] getMovementDataForDraw(float[] startPoint) {
     
  if (moves == null || moves.size() < 2)
   return null;
  
  if (this.isMovementStatisticsNeeded)
   this.movementStats.calculateMovementStatistics(moves);

  LinkedList points = convertMovesToPoints(startPoint);
  
  float[] limits = getMinMaxCoordsOfPoints(points);
  
  centerPathToScreen(points, startPoint, limits);
  
  LinkedList pointsFiltered = filterOutLinesWithSmallAngleChange(points);
  
  Path path = convertPointsToPath(pointsFiltered);
  
  Object[] ret = new Object[3];
  ret[0] = path;
  ret[1] = pointsFiltered.getLast();
  ret[2] = this.movementStats;
  
  return ret;
 }

I think that this peace of code is self-descriptive, so I will not make many comments on this :-)
And finally - some picture describing How this movement path looks like when application runs on Android-enabled device. Using this app I walked near the walls of my flat, so by doing this in the end we get my flat scheme, which looks like this:

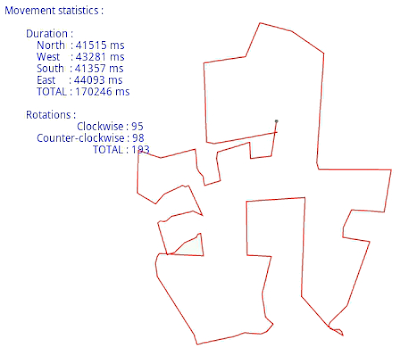
Some explanations,- starting from lower-right corner and going clockwise in picture you will get such rooms: kitchen, bedroom, WC, bathroom, sitting-room.

Have fun developing for Android and using sensors !

User identification by his/her keyboard typing pattern

I would like to show my next masterpiece :-) It would be about biometrics - How to identify a user by it's keyboard typing pattern. Basic approach is not very complex. At first you need to record typing duration of symbols in phrase which user types on keyboard. There are two kinds of typing duration - one is time between key press and key release events, and second - time between key presses of two adjacent symbols in typing phrase. So we accumulate these durations into some list or array and we will some sort of signal. We also need to modify this signal a bit, because it contains noise - some random fluctuation of user's typing pattern. So before we could use this duration info - there is intermediate step - convert typing durations signal into frequency domain using FFT transformation. After FFT tranformation we filter-out signal components with high frequency and convert back filtered signal from frequency domain into time domain by FFT transformation. Once we have typing durations with basic typing pattern with small amount of noise - we save this signal in file and later compare it with user's current typing duration pattern. So user identification algorithm is this:

1. Record current typing durations of symbols and durations between symbols in a typing phrase
2. Convert these durations signal into frequency domain using FFT
3. Filter-out high frequency signal components
4. Convert back signal from frequency domain into time domain
5. Compare this filtered signal with the one recorded from user previously and stored in file.

Some notes about step (5):
There can be multiple choices about how we can compare two signals. I have chosen simple approach - count How much slopes in these two separate curves has same direction, i.e. they both should increase or both should decrease. Number of same direction slopes is divided from total number of slopes and we get curves matching factor. When it will be bigger than some tolerance level - we can say that user who typed phrase is the same who typed previously recorded phrase. I have prepared proof-of-concept Java application which records/detects/shows user typing pattern. You can download it and as always - use as you wish. A little bit of explanation how Java code is structured:

FftBase.java

Helper.java

SimpleBiometricApplication.java

FftBase.java

has functions for performing direct and inverse FFT operation. I downloaded this module from this developer.

Helper.java

groups bunch of functions which are used together with FFT operation, such as "filterOutHighFrequencies" (removes high frequency noise from signal in frequency domain), "normalizeFftOutput" (scales Y axis of FFT operation into 0..1 range), "extractTypingPattern" (converts typing pattern into freq. domain, removes noise, converts back into time domain, scales output to 0..1 range and returns data to the user), "loadTypingPattern" (loads recorded typing pattern from CSV file into double array), "generateCsvFileForTypingDurations" (saves typing pattern into CSV file).

SimpleBiometricApplication.java

Swing application which uses above modules for recording/detecting user typing pattern. Typing patterns are also pictured in a graph using JfreeChart java library. It was my first experience with Swing. At first I thought to use JavaFX, which is cool also and more configurable than Swing, but at the moment I didn't found GUI builder for Fx and because Swing is well known and used in java developing industry - I decided to learn Swing a bit. It was nice experience that you can set custom code in Swing builder which modifies some GUI component property. I just miss the feature that this custom code editor could accept anonymous function for setting some property. Now it just accepts such arguments which are accepted by Swing component some "set..." method. Probably the problem was that at the time when Swing was written - java had no anonymous functions - they could came later. And custom code for setting some property can be lengthy. It is good when this swing component set... method accepts some class - when you can write in editor anonymous class and pass it to the custom code editor. But this not always helps, because accepted class in set method parameters can implement such interface from which you CAN'T cast back into class accepted by set method. For example - i needed to modify JFrame bounds property which accepts Rectangle. Rectangle implements Shape interface. So I thought I will pass custom anonymous class made from Shape into setBounds method accepting Rectangle. But I couldn't do that because the reason was that Shape can't be converted to Rectangle class, no matter that Rectangle itself implements Shape. Comma operator in Java would help also in this case, but we don't have comma operator (at least for now). But otherwise GUI builder is very helpful, has a lot of components.

And finally - how my Swing form looks like - when typing pattern is detected for the user:

If user is the same who typed original recorded message - you will see such messageBox:

For me most interested coding parts was related with FFT stuff and signal comparison. You should like it also !
Have fun in signal processing !

Reading between the lines

befoRe anna paVlOvNa And the otHers HaD timE tO smile their appreCiAtion of tHe ViCoMte's EpigRaM, Pierre aGaIn BrokE iNtO the CoNvErsation, AnD thoUgh Anna Pavlovna fElT sUre he wouLd Say sOmEthiNg InapPropRiate, she Was uNable tO sTop hIm. "ThE execution of thE DUc d'ENgHien," deClarEd monsIeur PierRe, "WaS a PoliTiCal nEcessity, And iT sEems to me thAt napoleon ShOwEd GreaTnEss of sOul by not FeArInG to take oN himSeLf thE wHoLe respOnsibiLity Of thAt deed." "DiEu! mon DIeu!" mUtTeRed ANnA PavLoVna in a teRrified whiSpEr. "What, MoNsieUr piErRe... Do you consider that assassination shows greatness of soul?

Can you guess what this text represents ? :-) It's extract from the book "War and Peace" but not only that. This peace of text holds secret message also. When this text is decoded it gives such secret message:

the quick brown fox jumps over the lazy dog.

So this time i would like to add new meaning to phrase "reading between the lines" in computing world. Actually it's better to say "reading between the chars" in this case :-) Talk will be about text steganography - how to hide some secret message, aka. payload in original text fragment. Idea is to modulate letter casing so that casing of letters itself in original text would carry additional information which can be used for example to encode some secret message in text. So at first you need to choose some prefixed alphabet of characters to be used in secret message. It's better to have small alphabet, because bigger set will result in a need for a longer original text so that it could contain all secret message. I've used these chars for secret message - 'qwertyuiopasdfghjklzxcvbnm. |'. It's 30 characters. So you need at least 30 different secret states to represent these characters in text. I've chosen letter case to represent this secret state. Upper case of letter means bit 1, lower case - 0. So by using such scheme you can encode 1 bit into letter casing of 1 character (or 2 total states - uppercase,lowercase). Next step is to calculate how much letters of original text you need to encode 1 secret letter by using such scheme. We need to multiply number of states of each letter, so if one letter holds 2 states, 2 letters holds 2*2=4 states and so on. So 5 letters holds 2*2*2*2*2 = 32 states or 5-bit integer of additional information which is enough for our 30 letters alphabet. This integer will represent our secret letter index in our alphabet. So for 1 secret char you need 5 original text chars. General encoding algorithm idea is this (decoding procedure is very similar just some steps are in reverse order):

1. Get next secret char from the secret message
2. Get secret char index in your alphabet
3. Decompose this index into 5-bit binary pattern
4. Encode this 5-bit pattern into 5 letters from original text using uppercase mode as bit 1, lowercase mode - as bit 0
5. Repeat everything from point 1 until all chars of secret message are encoded

I've prepared for this algorithm Java program, you can download it and use as you wish,- as always no restrictions applied - use at your own risk :-) . There are just two classes - Test.java is main program and TextSteganography.java is class which encapsulates encode/decode methods for secret messages. Class TextSteganography.java holds two most important methods - "modulateText" and "extractSecretMessage" which code is this:

    public String modulateText(String text, String hiddenText) {
        hiddenText += '|';
        char[] inp = text.toCharArray();
        char[] hidden = hiddenText.toCharArray();
        int letterIx = -1;

        CheckCondition(containsOnlyValidChars(hiddenText), String.format("Hidden text can only contain chars from the set '%s'", 
                                                                         validChards.substring(0, validChards.length()-1)));
        int letterCount = countLetters(text);
        CheckCondition(letterCount >= 10 * hiddenText.length(), 
                       String.format("Must be at least %d letters in text, but given %d for current payload message", 10 * hiddenText.length(), letterCount));
        
        for (int i = 0; i < hidden.length; i++) {
            int ix = validChards.indexOf(hidden[i]);
            String patternString = "0000" + Integer.toBinaryString(ix);
            char[] pattern = patternString.substring(patternString.length() - 5).toCharArray();
            boolean[] convertToUppercase = upperCaseIsNeeded(pattern);
            
            for (int j = 0; j < convertToUppercase.length; j++) {
                letterIx = getNextLetterIndex(inp, letterIx);
                inp[letterIx] = (convertToUppercase[j])? changeLetterCase(inp[letterIx], LetterCase.UPPER_CASE) : 
                                                         changeLetterCase(inp[letterIx], LetterCase.LOWER_CASE);
                letterIx = getNextLetterIndex(inp, letterIx);
            }
        }
        
        return String.valueOf(inp);
    }
        
    public String extractSecretMessage(String text) {
        LinkedList charList = new LinkedList<>();
        char[] inp = text.toCharArray();
        int letterIx = -1;
        int letterCount = 0;
        int binaryPattern = 0;
        int newBit;
        
        while (true) {
            letterIx = getNextLetterIndex(inp, letterIx);
            if (letterIx != -1) {
                letterCount++;
                newBit = (getLetterCase(inp[letterIx]) == LetterCase.UPPER_CASE)? 1 : 0;
                binaryPattern = (binaryPattern << 1) + newBit;
                
                if (letterCount == 5) {
                    char c = validChards.charAt(binaryPattern);
                    if (c != '|')
                        charList.add(c);
                    letterCount = 0;
                    binaryPattern = 0;
                    if (c == '|')
                        break;
                }
                letterIx = getNextLetterIndex(inp, letterIx);
            }
            CheckCondition(letterIx != -1, "Text was not encoded with this steganography encoder !");
        }
        
        return charListToString(charList);
    }

Some additional interesting comments. At first I wanted to use assertions in Java. But I've found information that assertions are not recommended in general, at least in production code. Besides they are turned-off by default in Java virtual machine. You need to turn them on by -ea switch. But I like assertions very much, because they gives you an opportunity to check some conditions in fast way without writing 'if(s)'. So I wrote function "CheckCondition" which is assert analog but acts in recommended way - throws an exception if condition is not met. Next interesting note - when I profiled an application I found that secret message extraction is relatively slow because each decoded character was appended to output string by StringBuilder. And that's natural, because as I've understood String is just a wrapper around char array. And as we know appending new array element is slow procedure, because you need to re-size array, copy elements to new array and etc, and this takes time. So instead I append new decoded characters into LinkedList of chars and later I converted this list into usual String. This approach works faster when you need to build new String incrementally. That's all.
Have fun in using text steganography !

Solving eight queens problem with random walk algorithm

Recently I wrote article about solving eight queens problem with electrical force analogy. But after thinking some time I came to conclusion that repulsion force from the board edges and repulsion force between queens will force queens to move in random fashion. So in general this queens behavior should be comparable to random walk algorithm. So seems that at least in this case concept of electric force is not needed - we should follow an Occams's razor principle and simply use random walk algorithm which will generate comparable results. Algorithm principle is very simple - one needs to have just a bunch of initial random values for some parameters (in queen case parameter would be X or Y position for the queen) and then in each subsequent iteration one just needs to apply some small random shift to each parameter value until solution is found. So this random walk concept I implemented in latest Java eight queens solver which you can download and use without restrictions. Code structure:

- JavaEightQueensProblem.
Main class which employs random walk algorithm for solving eight queens problem.

- RandomWalkerParameter.
Class which holds random value to shift in each algorithm iteration. Besides it holds two ranges - random value range, which defines number limits for random value and shift step range, which defines number limits for shift step. In each iteration random shift step is added to current random value.

- RandomWalkerUnit.
Class holding list of random walk parameters and state which defines unit has reached terminating value or not. If unit has reached terminating value - subsequent random shifts are not applied to unit parameters. Basically this class is just needed for grouping parameters. For example queen random unit will have two parameters - X,Y. So in queen case both values X,Y will be randomly mutated until queen will reach good position on board. So calculation terminating condition is meaningful only for X,Y pair - i.e. random unit will have two X,Y parameters in list for queen problem case.
- RandomWalker.
Class which executes random walk algorithm. Most important things which should be passed into RandomWalker constructor is: list of random walker units and object which will have method for checking if random walk unit has reached terminal state or not. This method will be then executed dynamically by using java reflection in each subsequent random walk iteration. By the way, you can pass class instance OR class itself into this calculator object parameter. Passing class itself is good if your terminal condition calculation method is static - so in this case you don't have to create class instance for calling method and thus it is reasonable for random walk constructor to accept class object itself. Next when random walker object is constructed one just needs to execute one method named "startRandomWalkSearch()" to begin looking for solution to some problem. This random search algorithm has no special magic in it :-), basic code is simple like this:

    public void startRandomWalkSearch() {
        Random rnd = new Random();
        int iterationsUntilRestart = 0;
        
        initializeRandomWalkUnits();
        for (int i = 0; i < iterationsToTry; i++) {
            iterationsUntilRestart++;
            
            if (unitsNotInTerminalState == 0) {
                iterationsUntilSolution = i + 1;
                return;
            }          
            
            if (iterationsUntilRestart > restartRandomWalkAfterIterations) {
                iterationsUntilRestart = 0;
                initializeRandomWalkUnits();
                continue;
            }
            
            for (int iUnit = 0; iUnit < randomWalkUnits.size(); iUnit++) {
                if (!randomWalkUnits.get(iUnit).terminalConditionReached) {
                    
                    for (RandomWalkerParameter randomWalkParameter : randomWalkUnits.get(iUnit).randomWalkerParameters) {
                        double stepValue;
                        double stepValueDiff = randomWalkParameter.stepRange[1] - randomWalkParameter.stepRange[0];

                        // calculate step value
                        if (randomWalkParameter.onlyIntegralValuesInStep)
                            stepValue = randomWalkParameter.stepRange[0] + (double)rnd.nextInt((int)(stepValueDiff + 1.0));
                        else
                            stepValue = randomWalkParameter.stepRange[0] + stepValueDiff * rnd.nextDouble();

                        // apply step
                        randomWalkParameter.value += stepValue;
                        randomWalkParameter.value = Math.min(randomWalkParameter.value, randomWalkParameter.valueRange[1]);
                        randomWalkParameter.value = Math.max(randomWalkParameter.value, randomWalkParameter.valueRange[0]);

                    }
                    // check terminal condition
                    Class[] types = new Class[2];
                    types[0] = List.class;
                    types[1] = int.class;
                    try {
                        boolean isJavaClass = terminalConditionCalculatorObject.getClass().toString().contains("java.lang.Class");
                        Method method;
                        if (isJavaClass)
                            method = ((Class)terminalConditionCalculatorObject).getMethod(terminalConditionCalculatorMethod, types);
                        else
                            method = terminalConditionCalculatorObject.getClass().getMethod(terminalConditionCalculatorMethod, types);
                        
                        randomWalkUnits.get(iUnit).terminalConditionReached = 
                                                        (boolean)method.invoke(terminalConditionCalculatorObject, randomWalkUnits, iUnit);    
                        if (randomWalkUnits.get(iUnit).terminalConditionReached)
                            unitsNotInTerminalState--;
                    } 
                    catch ( NoSuchMethodException | 
                            NullPointerException | 
                            SecurityException | 
                            IllegalAccessException | 
                            InvocationTargetException e) {
                        throw new RuntimeException(e.toString());
                    }
                }
            }
        }
    }

Algorithm idea is to initialize each unit's parameters to some random value. Then there is for loop which applies small random step to parameter value and then checks if this unit has reached terminal(solution) state or not, by calling terminal condition calculation method using reflection.
And there is some unit test package which checks if random walk algorithm works - if you will want to modify algorithm. So you will need to see if random walk has good integrity after that or not :-) There is just one test package:

- RandomWalkerTest.
. What it does is - creates random walk object for performing random search if some number X can be factorized into A * B. This test package has two tests inside - testRandomWalkSearchNumberWasFactorized which tests if number was factorized correctly and test named testRandomWalkSearchNumberWasNotFactorized which expects that factorization must fail, because we pass prime number for factorization, which of course can't be factorized into smaller parts.
Have fun in using random walk search algorithm !!

Solving eight queens problem with electrical force analogy

In this problem I wanted to design and test some innovative algorithm approach for finding solution to eight queens puzzle. Algorithm idea is based on electrical force analogy. Hypothesis for algorithm design was that if queens are affected by some electrical field which pushes queens from each other by some law - after some iterations queens should arrange into stable positions which will compose solution. Idea was successful. But for this algorithm to work one needs 3 repulsion forces: - electrical force. (Two queens pushes themselves apart so that distance between them increases. Imagine queens as some electric particles of same charge, for example electrons :-) ).
- repulsion from same line. (If two queens share same horizontal,vertical or diagonal - they pushes each other so that they must leave same line.)
- repulsion from board borders. (Borders are imagined as same charge particles as queens, so borders pushes queens to the center of board.)
Below are pictures which graphically represents these 3 pushing forces. Forces are pictured as vectors by which green queen affects blue queen.

Electrical force:


Repulsion from same line force:

There are six possible repulsion directions from the line occupied by two queens. Currently algorithm calculates these six repulsion directions and takes one random direction from those six. Not all directions are equal. It can be that those two queens may be moved to other line at next iteration. So algorithm may be improved to skip directions which forms other common line between those two queens. But this improvement was not in the scope of this article :-)

Repulsion from board borders:

It was imagined that borders pushes queens to the center of board - as board would be a circle, not a rectangle. So this approximation is not very accurate - next improvement for algorithm :-) But for this scope that approach is good enough and works. So in the end superposition of these three forces accumulated from all queens and borders pushes targeted queen into right position - partial solution of eight queens problem. And finally we get solution. Algorithm was developed with JAVA programming language. This is my first experience with JAVA, so don't expect nice OO patern :-) I was developing with NetBeans IDE, which is a great tool for JAVA. You can download this solution and use as you need from here. Class structure of JAVA project is following:

- ChessBoard.
Holds information about queens, chess board representation data for printing board to output, groups code which targets queen objects.

- CollisionDetector.
Very small class which actually holds just one function "hasCollision" for calculating are two queens on the same position.

- EightQueensSolver.
Abstracts solution problem at a highest level. Most important method is SolveEightQueensProblem() which is structured as following:

    public boolean SolveEightQueensProblem() {
        final int totalIterations = 10000;
        boolean found;
        
        for (int iterations = 0; iterations < totalIterations; iterations++) {
            findMaximumTwoWrongQueens();
            if (currentWrongPositions == 0)
                return true;
            if (currentWrongPositions == 1) {
                found = findBruteForceSolutionFor1Queen();
                if (found)
                    return true;
            }
            if (currentWrongPositions == 2) {
                found = findBruteForceSolutionFor2Queens();
                if (found)
                    return true;
            }
        }
        return false;
    }

All our algorithm magic goes into function "findMaximumTwoWrongQueens()" - where by using above mentioned forces algorithm finds out at most two queens in wrong positions and then later SolveEightQueensProblem() performs brute force on those two queens positions. findMaximumTwoWrongQueens is structured as following (not very important code here is skipped for representing reader most useful algorithm part.):

    private void findMaximumTwoWrongQueens() {
        final int iterationsForTwoWrongPositions = 300;

        currentWrongPositions = 8;
        
        while (currentWrongPositions > 2) {
            chessBoard = new ChessBoard();
            chessBoard.RandomlyPlaceEightQueens();

            for (int i = 0; i < iterationsForTwoWrongPositions; i++) {
                chessBoard.ApplyElectricForce();
                chessBoard.UpdateChessBoard();
                currentWrongPositions = chessBoard.numberOfQueensInWrongPositions();
                if (currentWrongPositions < 3)
                    break;
            }            
        }        
    }

Here most interesting code is function ApplyElectricForce() which calculates new movement direction for each queen by calling method CalculateGlobalMovementDirection(Queen, ChessBoard). Method CalculateGlobalMovementDirection() is structured as following:

    public Tuple CalculateGlobalMovementDirection(Queen queen, ChessBoard chessBoard) {
        Tuple direction = Tuple.zeroTuple;
        Tuple directionInfluenceZoneRepulsion = Tuple.zeroTuple;
        Tuple directionElectricForceFromQueen = Tuple.zeroTuple;
        Tuple directionElectricForceFromBoardBorders = Tuple.zeroTuple;
         
        if (queen == null)
           throw new RuntimeException("queen is null");
         
        if (chessBoard == null)
         throw new RuntimeException("chessboard is null");
                
        for (int i = 0; i < 8; i++) {
            if (queen.Id.equals(chessBoard.queens[i].Id) == false) {
                directionInfluenceZoneRepulsion = RepulsionFromTheSameLineDirectionFromAnotherQueen(queen, chessBoard.queens[i]);
                directionElectricForceFromQueen = ElectricForceDirectionFromAnotherQueen(queen, chessBoard.queens[i]);
                
                if (Tuple.AreTuplesTheSame(directionInfluenceZoneRepulsion, Tuple.zeroTuple))
                    directionElectricForceFromQueen = Tuple.zeroTuple;
                
                direction = Tuple.AddTuples(direction, 
                                            Tuple.AddTuples
                                                (
                                                 Tuple.multiplyScalar(6,  directionInfluenceZoneRepulsion),
                                                 Tuple.multiplyScalar(2,  directionElectricForceFromQueen)
                                                )
                                            );
            }
        }
        
        // add borders effect
        directionElectricForceFromBoardBorders = ElectricForceDirectionFromBoardBorders(queen);
        direction = Tuple.AddTuples(
                                    Tuple.multiplyScalar(1,   direction), 
                                    Tuple.multiplyScalar(5,   directionElectricForceFromBoardBorders)
                                    ); 
                
        return Tuple.NormalizeTuple(direction);
    }

This method is the key to success of our algorithm and is most important code part.

- Geometry.
This class abstracts methods for detecting if two queens are on the same line - be it horizontal,vertical or diagonal.

- JavaEightQueensProblem.
Class which holds main() method, i.e. main program.

- Queen.
Very tiny class which just abstracts some queen attributes such as queen identification on board, queen position, queen movement direction and queen state determining if it reached position not influenced by other queens or not.

- RepulsionForce.
This class has several very important methods: ElectricForceDirectionFromAnotherQueen - calculates direction of target queen affected by source queen electrical force; RepulsionFromTheSameLineDirectionFromAnotherQueen - calculates direction of target queen affected by source queen force which pushes queen from the same line; ElectricForceDirectionFromBoardBorders - calculates direction of target queen affected by board borders electrical force which pushes queen towards the center of board; CalculateGlobalMovementDirection - calculates direction of target queen which is aggregation of all directions produced by forces of 7 other queens and direction produced by board borders repulsion force.

- Tuple.
Helper class which introduces Tuple abstraction and methods which groups vector algebra operations. Here Tuple is used as vector in plane.
That's it about solution code. Now I think it would be fun to see some movie of solution formation under effect of repulsion forces. On each algorithm run some random solution is found. Here it is my favorite one:

So in this algorithm run after 1397 iterations queens arranges into such beautiful solution lattice:


Conclusion:
Seems electrical force analogy is useful for solving eight queens problem and may be useful too for solving other general problems where not exists exact algorithm for finding solution, but some general algorithms are used - such as genetic algorithms, genetic programming, etc. One just needs to make a good abstraction for repulsion/attraction forces which pushes problem state from bad solutions or attracts towards better partial ones.
Have fun using electrical force analogy in algorithms !

Smoking effects on cigarette filter color

This time I will present some mini research about how smoking induces filter color changes. Experiment was following - I made cigarette filter photograph after each inhalation with camera. Later these filter pictures were processed with C++ program to determine filter average normalized opacity and how it changes with relation to inhalation number. You can download this C++ program which analyzes this effect from here. This zip includes C++ project itself and PGM pictures of cigarette filter shot after each inhalation. C++ project is simple - it just has following parts:

- pgmImage class which has loading and saving methods for PGM image type.
- cigaretteFilterAnalyzer class which basically calculates normalized averaged filter opacity in each image.
- cigaretteFilterEffects.cpp program itself which outputs experiment data on stdout.

Basic effects as it should be of course is that with each inhalation filter gets darker and darker. I compiled 13 pictures into one to show this effect:

Number below each filter image represents inhalation number. In addition to visual appeal of this effect I made plot from the experiment data processed with C++ program. You can see this plot how filter opacity changes over inhalation number here:

In this graph I added linear data fit. Linear data fit has R^2 of 0.95, so it seems that linear fit describes opacity changes pretty well. What is interesting that given relative filter opacity you can deduce how many inhalations was taken. I bet there can be more interesting ideas to explore which even further expands on research,- for example this effect should depend on filter quality. So basically some research can be done to explore how filter quality affects opacity effect. Which could be interesting to cigarette manufacturers. But that is just a guess. Also this effect should depend on filter structure, size, cigarette type, materials being used, inhalation duration, etc. For example cigarettes used for this experiment were with menthol capsule, so some additional effect arrived which relates how smoke propagates through menthol capsule. Also below is interesting picture about how cigarette filter looks like without smoking:

Filter picture was converted to gray-scale and histogram equalization method was performed on image to amplify color differences between pixels. Because some color changes are too small for an eye to see, but after histogram equalization it is easy to see smaller differences of pixels. After performing this we get nice picture of filter porosity :-) As I've said these cigarettes were with menthol capsule. So bellow is also one image after 12 inhalations converted to gray-scale and with histogram equalization performed:

Some lines were added to indicate menthol capsule. It can be clearly seen that capsule has strait in the middle - it is the place where it was crushed with the fingers before smoking. Otherwise you will not get menthol taste :-) At first I haven't understood why such shape appears in almost all pictures. I thought that we get concentric darker zone in the filter middle just because somehow smoke propagates better through the center of filter. But for this being true, there must be some randomness in each filter picture, because you can't guarantee that in each inhalation smoke will propagate in the same way. But in contrary this shape was too clear and similar between all images. So just very determined situation can induce the same shape effect. Best explanation was menthol capsule effect. Maybe there are more explanations - I don't know :-) This is it. People who smokes can make similar experiment themselves. But I bet it is better not to smoke at all because not just the opacity of filter changes but there are more serious effects on health too. And this opacity effect shows indirectly this too, because the reason why opacity gets greater with each inhalation is that filter becomes more polluted with each inhalation. So you better stop smoking :-) Regards, Agnius

ASP.NET web site for generating test data

Have you ever wanted ASP.NET site (and it's source code) with functionality as in generatedata.com (which aims at generating test data) ? If so - just check my newest creation at codeplex. License is MIT, so you can use it as you wish. Have fun at generating test data ! Best wishes, Agnius